
Analogy, and the like
IGS - Intelligent and Graphical Systems Research Group
Analogy is a very flexible mode of reasoning. Consider the following analogies:
123 is to 124 as 789 is to__
abc is to ddab as wxy is to __
dog is to bark as cat is to __
pen is to write as gun is to __
solar-system is to sun as atom is to __

Analogies are often asymmetric, consider the difference between:
"A man is like a pig" - - - presumably, unclean, untidy, smelly, etc.
and
"A pig is like a man" - - - indicates that pigs are intelligent, inquisitive, etc.
See my lecture notes on Models of Analogy in postscript format.
The first two IQ-test problems below require matching objects and attributes (Evans, 1967). But adding colours and patterns (ie attributes) does not necessarily follow the same pattern.
1) Local attribute Matching: Most Geometric Analogy problems, the objects plus their attributes are "bound together", and treated as a unit.
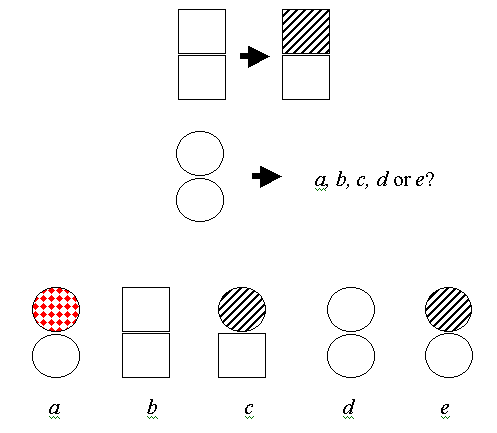
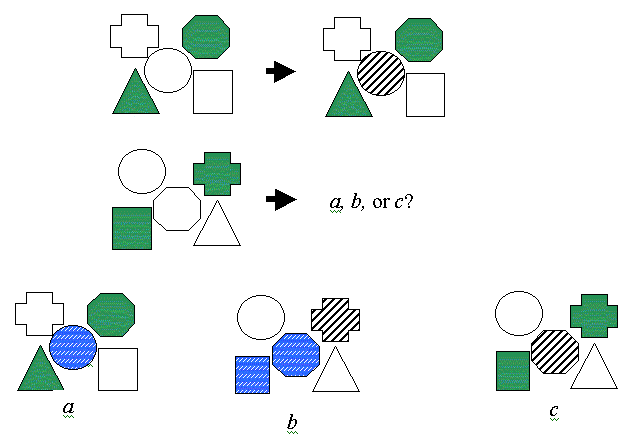
2) Global attribute Matching:
However, more complex analogies treat the objects and attributes as mutually independent entities.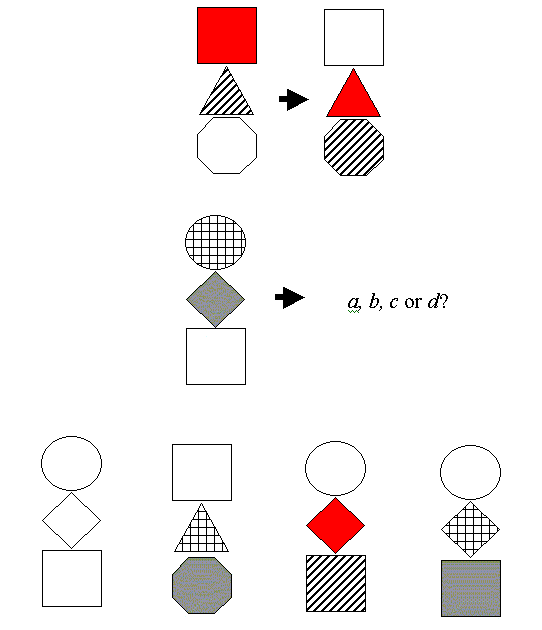
The last problem is very complex, involving a number of independent mappings, with a large potential for conflict. We require
(at least) two very different algorithms to solve these two different types of analogy problem. (paper.pdf)|
Model |
Author(s) |
Model |
Author(s) |
|
( Forbus, Gentner) |
( Thagard, Holyoak) |
||
|
IAM |
( Keane) |
( Veale) |
|
|
Lisa |
( Hummel, Holyoak) |
( Mitchell, Hofstadter) |
|
|
(Evans '67) |
( Petrov, Kokinov) |
|
ARCS -a cousin of ACME |
(Thagard, Holyoak, Nelson, Gochfeld) |
MAC/FAC -SME's cousin |
( Gentner, Forbus) |
|
( Plate) |
|
|
|
|
|||
|
|
|
|
The goal: To produce a computer model of how people reason with analogies.
The analogy process is typically decomposed into five phases of representation, retrieval, mapping, transfer and induction (Keane et al, 1994).
Mapping is the key stage, and this uses graph Identicality as the basis to find the comparison. The following diagram shows the graph alignment for the famous "John F. Kennedys' White House was like Camelot" analogy.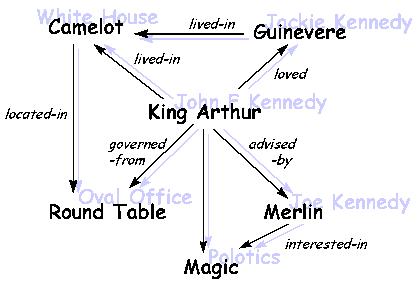
Apparently simple sentences often contain a wealth of information which must be deciphered, before the real meaning is identified. This happens transparently in people, but is very difficult to replicate on computer.
Analogies (and Metaphors) are composed of two unequal parts:
SOURCE containing much knowledge and is the concept from which we learn (Camelot)
TARGET containing a little knowledge and about which we want to learn more. (JFK)
"John F. Kennedys' White House was like Camelot " is a frequently cited analogy. Predicate Calculus assertions describe facts known about the source (Camelot) and target.
Computational models of Analogy require many distinct though interrelated processes; Representation, Retrieval, Mapping, Validation, Transfer and Induction. SYSTEMATICITY is the Key concept to understanding Analogies. This is the identification of similar or matching structures between the Source and Target.
Identify matching (Mapping) between concepts from the Source and Target. Identify structures in the Source which are not in the Target. This "missing" information in the Target is the basis for Analogical Learning.
Existing computational models of Analogical Reasoning (SME, ACME, IAM) are based on the Systematicity principle to perform the Analogical Mapping process. SME generates all possible solutions in a Depth-First Search manner, storing the largest Sytematic solution found so far. ACME dynamically generates a neural network representing the entire solution space, and mutual support and coonpetition between solution elements causing the network to settle into a stable state representing the largest thematic solution. IAM generates a seed mapping which is grown incrementally until the final solution is produced.
From a pure Computer Science perspective, this work centres on a variety of algorithms for tree or graph matching - generating large trees of match hypotheses between Source and Target, finding the largest consistent structure mapping between Source and Target. This work involves a variety of architectures - Neural Networks, Localist-Connectionist models, as well as traditional Symbol manipulation approaches. Many models integrate more than one of these architectures.
Related Analogy and Metaphor web sites (references)