T Naughton, CS NUIM, Back to SE307 home

Q1 One such pushdown automaton is

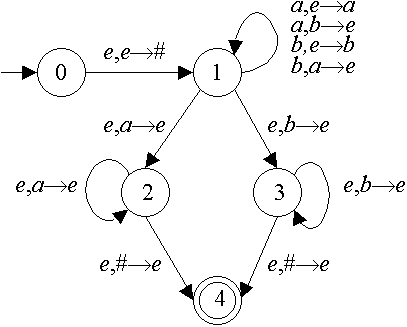
Marking scheme:
Any correct automaton: 3 marks
One or two incorrect or missing transitions: 2 marks
Three or four incorrect or missing transitions: 1 mark
Otherwise: 0 marks

Q2 Possible solutions include

S->aSb|Sb|b

or

S->aBb
B->Bb|b

Marking scheme:
Any correct grammar: 2 marks
One or two small mistakes (such as generating e): 1 mark
Otherwise: 0 marks

Q3 The languages L = {aⁿbⁿ : n>=0}, L = {w : wÎ{a,b}*, w contains the same number of as as bs}, and L = {wxw^R : wÎ{a,b}*} are context-free languages that can be accepted by a deterministic PDA. The languages L = {a^mbⁿc^p : m,n,p>=0, m=n or m=p} and L = {ww^R : wÎ{a,b}*} are context-free languages that cannot be accepted by a deterministic PDA.

Marking scheme:
One mark for an example of each type (2 marks maximum)

Q4 (i) Prove that all regular languages are context-free. This could be done by showing that a PDA can simulate a FA, or by showing that a CFG can generate any regular expression.
(ii) Show that a particular language L is not regular. This could by defining L clearly and then using a pumping lemma proof.
(iii) Show that L is context-free. This could be done by showing how L could be generated with a CFG or constructing a PDA to accept L.

Marking scheme:
One mark for describing each proof (3 marks maximum). A half mark will be awarded if the proof is stated but not explained.

Q5 To prove that any machine A is no more powerful than machine B, we have to prove that B can simulate the actions of A. In this case we would have to show that a 2-stack PDA can simulate any n-stack PDA for any n>2.

Marking scheme:
Stating that a simulation is required: 1 mark
Otherwise: 0 marks

Q6 Option (ii) is the easiest. Order the finite-length decimal numbers between 0 and 1 according to the following rules: (a) shorter numbers come first, and (b) if two numbers have the same length then the smaller number comes first. These rules form an unambiguous way to order the numbers. Given these rules we'll end up with an ordering such as:

0
1
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
0.01
0.02
0.03
0.04
.
.
.

If we associate the first number with 0, the second with 1, the third with 2, and so on, we will have found a bijection with the natural numbers and proved that the set of finite-length decimal numbers between 0 and 1 is countable.

Marking scheme:
Correct proof: 2 marks
Right idea but some mistakes: 1 mark
A lot of mistakes or wrong idea: 0 marks

Q7 Examples include a^2pb^p or a^pb^pa^p or a^pb^p/2 or b^pa^2p.

Marking scheme:
Any two correct examples: 2 marks
One correct example: 1 mark
Otherwise: 0 marks