T Naughton, NUIM
Back to SE307 home

Lab 7 - Pushdown automata

Note: if you don't finish a laboratory assignment within the scheduled laboratory hours, it is expected that you finish it in your own time. This, of course, goes for problem 6.1 from last week.

As explained in lectures, a language is a CFL (context-free language) iff it is accepted (recognised) by a PDA (pushdown automaton). Therefore the existence of a PDA to accept a particular language L serves as a proof that that language is a CFL. An example follows. Note the phrases and logical statements that is used in formal proofs. Practise using these logical statements in this lab to become familiar with them. You do not need your PC for this lab.

Problem 7.A Let L_A={aⁿbⁿ : n>=0}. Prove that L_A is a CFL.

Proof 7.A I choose to prove L_A is a CFL by proving the existence of a PDA that accepts L_A. Let M be the following PDA:

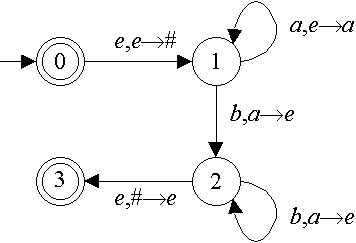
M accepts L_A, and M is a PDA, and there is a theorem that says that if a PDA accepts a language then that language is a CFL, therefore this proves that L_A is a CFL.

Problem 7.1 Let L₁={ww^R : wÎ{a, b}*}. Prove that L₁ is a CFL.

Problem 7.2 Let L₂={wcw^R : wÎ{a, b}*}. Prove that L₂ is a CFL.

Problem 7.3 Let L₃={w : wÎ{a, b}*, w=w^R}. Prove that L₃ is a CFL.

Problem 7.4 Let L₄={a^mbⁿ : m,n>=0, m=2n}. Prove that L₄ is a CFL.

Problem 7.5 Let L₅={w : wÎ{a, b}*, w has twice as many as as bs}. Prove that L₅ is a CFL.

Problem 7.6 Let L₆={w : wÎ{a, b}*, w contains the substring aab}. Prove that L₆ is a CFL.

Problem 7.7 Prove that all regular languages are context-free. You should use a "constructive proof" that consists of an unambiguous sequence of steps to turn any FA into a PDA that accepts the same language. (Use the same kind of reasoning you used to embed a FA into a TM.)

Problem 7.8 For each L_i defined in this lab sheet, specify a CFG (context-free grammar) that generates L_i.