CS605 - Mathematics and Theory of Computer Science

NUIMCrest CS605 - Mathematics and Theory of Computer Science
Maynooth University Department of Computer Science

Laboratory sheet - Finite automaton emulator

This lab sheet introduces an emulator for finite automata. We will use Paul Ming's Perl-based Virtual Turing Machine adapted for deterministic finite automata.

This lab sheet contains two examples, followed by a list of machines that you must construct yourself.

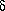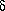Example Machine 1.A A FA that accepts the language L = {w : w $in$ {a, b}*, w ends with an a}. One FA that accepts this language is M = (Q, $Sigma$ , $delta$ , q₀, F) where Q = {00, 99}, $Sigma$ = {a, b}, q₀ = 00, F = {99}, and $delta$ is given by the transition function:

Q\ | a b ----------- 00 | 99 00 99 | 99 00

which could be formatted equivalently as follows by writing each transition on a separate row:

Q | | d(Q, ) --------------- 00 | a | 99 00 | b | 00 99 | a | 99 99 | b | 00

Simulate this machine with the VFA by using the following steps.

Open the virtual finite automaton (VFA) in a window on its own to give you some comfort.

Type "baba" (without quotes) as the input word. Spaces are ignored.

Type "00" (without quotes) as the start state.

Type "99" (without quotes) as the accept states.

Copy and paste the following code as the transitions.

00, a, 99 00, b, 00 99, a, 99 99, b, 00

Run the VFA. The output will include a trace of each step of the computation. Each line of the trace contains the current state of the machine, followed by the input word. The angled brackets < > indicate what is the next symbol that will be read from the input. The state that the machine halts in can be read from the last line of the trace.

Try various correct and incorrect inputs, such as "b", "ba", and "bbbbbba" (all without quotes) to satisfy yourself that the transition function of this machine is correct. Try the empty word too (nothing, or just empty spaces, as the input word).

Note, as a convention, let's label all accepting states 99,98,97,...,90 (even if the start state is an accepting state). This way it will be instantly possible to tell if the FA has accepted the word or not.

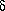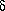Example Machine 1.B A FA that accepts the language L = {w : w $in$ {0, 1}*, w begins with a 1}. One FA that accepts this language is M = (Q, $Sigma$ , $delta$ , q₀, F) where Q = {00, 01, 99}, $Sigma$ = {0, 1}, q₀ = 00, F = {99}, and $delta$ is given by the transition function:

Q\ | 0 1 ----------- 00 | 01 99 01 | 01 01 99 | 99 99

which can be reformatted for the VFA as:

00, 0, 01 00, 1, 99 01, 0, 01 01, 1, 01 99, 0, 99 99, 1, 99

Paste it into the emulator and satisfy yourself that it works.

Additional languages recognised by example finite automata are available if you require additional self-study.

Below are a selection of problems that you could use to test your FA programming skills. Use the emulator to test sample inputs.

Machine 1.1 Construct a FA that accepts the language L = {w : w $in$ {a,b}*, w contains the substring aa}.

Machine 1.2 Construct a FA that accepts the language L = {w : w $in$ {0,1}*, w contains no 0s}.

Machine 1.3 Construct a FA that accepts the language L = {w : w $in$ {0,1}*, w does not begin with a 1}.

Machine 1.4 Construct a FA that accepts the language L = {w : w $in$ {a, b}*, w contains the substring baa but does not contain it at the very beginning of the word}.

Machine 1.5 Construct a FA that accepts the language L = {w : w $in$ {0,1}*, w contains at least one 0, w contains an even number of 1s}. Note: zero is an even number.

Machine 1.6 Construct a FA that accepts the language L = {w : w $in$ {a,b}*, w does not begin with ab}.

Machine 1.7 Construct a FA that accepts the language L = {w : w $in$ {a,b}*, w ends with the substring baa}.

Machine 1.8 Construct a FA that accepts the language defined by the regular expression (1 $union$ 0)0*.

Machine 1.9 Let $Sigma$ = {0, 1}. Construct a FA that accepts the language defined by the regular expression {} $union$ e $union$ $Sigma$ $union$ $Sigma$ $Sigma$ .

Machine 1.10 Let $Sigma$ = {0, 1}. Construct a FA that accepts the language defined by the regular expression $Sigma$ (0 $union$ 11 $union$ 111)* $Sigma$ *.

Machine 1.11 Let $Sigma$ = {a, b}. Construct a FA that accepts the language defined by the regular expression e $union$ $Sigma$ $union$ (a $Sigma$ *a) $union$ (b $Sigma$ *b).

End of sheet