T Naughton, CS NUIM, Back to CS403 home

Remove everything from your desk except pens/pencils. Paper will be provided. Answer all questions. Remember to be mathematically precise in all of your answers. You have until 15:50. You can leave whenever you are finished.

Note: Finite automata are deterministic by default.

Q1 Construct the state diagram for a finite automaton that accepts the language L = {w : wÎ{a,b}*, w is empty or contains the substring aab}. [2 marks]

Q2(a) Construct the state diagram for the finite automaton M written formally as M = (Q, S, d, q₀, F) = ({0, 1, 2, 3}, {a, b}, d, 0, {2, 3}) where d is

Q\S| a b
---------
 0 | 0 1
 1 | 2 1
 2 | 3 2
 3 | 2 3
[2 marks]

Q2(b) What language does the machine in Q2(a) accept? [1 mark]

Q2(c) If we change F to be F={1, 2} in the machine in Q2(a), what are the first 6 words in the lexicographical ordering of the new language accepted by the machine? [1 mark]

Q3 Describe with an English sentence the language accepted by the finite automaton M = (Q, S, d, q₀, F) = ({00, 01, 99}, {0, 1}, d, 00, {00}) where d is

Q\S |  0  1
-----------
 00 | 01 00
 01 | 99 01
 99 | 99 99
[2 marks]

Q4 The state diagram of finite automaton M is given below. Describe with an English sentence the language accepted by M.

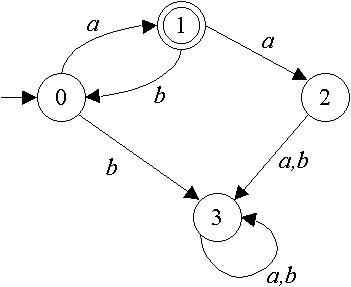[2 marks]

Q5 Let finite automaton M be written formally as M = (Q, S, d, q₀, F) = ({00, 01, 99}, {a, b}, {((00, a), 01), ((00, b), 99), ((01, a), 01), ((01, b), 00), ((99, a), 99), ((99, b), 00)}, 00, {99}). Construct a table of behaviour of a Turing machine within which the transition function d of M is embedded. State clearly the starting state and accepting states of the resulting Turing machine. [2 marks]