
|
CS403 - Computational Complexity Theory
Class test 2 (repeat)
Tuesday 23 January 2001, 16:00, Lab 2
|
T Naughton, CS NUIM,
Back to CS403 home
Remove everything from your desk except pens/pencils. Paper will be provided. Answer all questions. You have 50 minutes in total.
Use the MCQ answer sheet for Section B. Write both your name and student id. number on the MCQ sheet (remember to precede your number with a zero). Each MCQ question has only one fully correct option. Negative marking will be enforced: +1 for a correct answer, -0.25 for an incorrect answer, 0 for a non attempt. This means that randomly guessing answers will average a mark of zero.
Student's name..............................................................Student's number..............................................................
HAND UP THIS QUESTION SHEET WHEN FINISHED.
Section A – Turing machine programming
Q1 Write a two-tape Turing machine that counts the number of occurances of the substring "10" in its input. Initially, the TM head will be at the beginning of the input. At halt, the TM head must be at the beginning of the output. For simplicity, the output can be expressed in unary. For example, input "110011" would result in output "1", input "10010" would result in output "11", and input "0011" would result in output " ". Explain the purpose of each TM state in your comments.
Section B – Computability and complexity
Q1 What did Gödel prove?
(a) no sufficiently powerful formal system can be both consistent and complete
(b) no sufficiently powerful formal system can be both decidable and complete
(c) there is no decision procedure for arithmetic
(d) no sufficiently powerful formal system can be both consistant and decidable
(e) none of the above
Q2 As a direct result of one of Gödel's theorems, we can say that in order to build a pocket calculator that...
(a) never answers incorrectly, it must leave some questions unanswered
(b) can answer all questions, it must contradict itself
(c) never contradicts itself, it must leave some questions unanswered
(d) all of the above
(e) none of the above
Q3 Which of the following models of computation is more powerful (in terms of computability) than the others?
(a) a Turing machine with a 2-D tape, infinite in all directions, for its tape head to move over
(b) a random access machine with an infinite number of registers
(c) the Java programming language (assuming infinite available memory)
(d) partial recursive functions
(e) they all have equal power
Q4 The set of accepting Turing machines coincides with which of the following sets?
(a) the set of halting C++ programs
(b) the set of recursive functions
(c) the set of recursive languages
(d) the set of recursively enumerable languages
(e) none of the above
Q5 The set of recognising Turing machines does not coincide with proper subsets of which of the following sets?
(a) the set of partial functions
(b) the set of recursive functions
(c) the set of partial recursive functions
(d) the set of recursively enumerable languages
(e) none of the above
Q6 The computational complexity class PTIME, often referred to as P, ...
(a) defines a lower bound on the complexity of Turing machines deciding these languages
(b) defines a lower bound on the complexity of Turing machines accepting these languages
(c) defines a upper bound on the complexity of Turing machines deciding these languages
(d) defines a upper bound on the complexity of Turing machines accepting these languages
(e) none of the above
Q7 Does the class LOGTIME exist?
(a) yes, but only if Church's thesis holds
(b) no, but only if we assume a TM's input is not included in its space measure
(c) yes, but only if LOGSPACE exists
(d) no, but for a different reason to those above
(e) yes, but for a different reason to those above
Q8 Given the diagram below, depicting sets XÍYÍZ and elements aÎX, bÎY, cÎZ, which of the following statements is false?
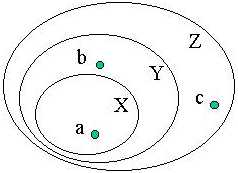
(a) a is X-hard
(b) b is X-complete
(c) c is Z-complete
(d) c is Y-hard
(e) none of the above


