
|
CS403 - Computational Complexity Theory
Class test 2
Tuesday 12 December 2000, 14:00, SLT
|
T Naughton, CS NUIM,
Back to CS403 home
Remove everything from your desk except pens/pencils. Paper will be provided. Answer all questions. You have 50 minutes in total.
Use the MCQ answer sheet for Section B. Write both your name and student id. number on the MCQ sheet (remember to precede your number with a zero). Each MCQ question has only one fully correct option. Negative marking will be enforced: +1 for a correct answer, -0.25 for an incorrect answer, 0 for a non attempt. This means that randomly guessing answers will average a mark of zero.
You may keep this question sheet when finished. Solutions will be provided within one week.
Section A – Turing machine programming
Q1 Write a one-tape Turing machine to reverse a binary string. Initially, the TM head will be at the beginning of the input. At halt, the TM head must be at the beginning of the output. For example, input "110" would be transformed into "011". Explain the purpose of each TM state in your comments.
Q2 Write a two-tape version of Q1.
Section B – Computability and complexity
Q1 What did Gödel prove?
(a) The incompleteness of mathematics is something that cannot be proved
(b) There will always be unsolvable problems in mathematics
(c) There is no way to remove contradictions from sufficiently powerful mathematical systems
(d) All of the above
(e) None of the above
Q2 For what is Church known?
(a) He defined `algorithm' in terms of his lambda calculus
(b) His lambda calculus is powerful enough to express all of mathematics
(c) Along with Gödel and Turing he showed that all mathematical systems are either inconsistent or incomplete
(d) All of the above
(e) None of the above
Q3 Which of the following models of computation is less powerful than the others?
(a) 1-tape Turing machines whose tapes are infinite in one direction only
(b) random access machines with finite numbers of registers
(c) lambda calculus
(d) partial recursive functions
(e) they all have equal power
Q4 The set of accepting Turing machines does not coincide with which of the following sets?
(a) the set of random access machines
(b) the set of recursive functions
(c) the set of partial recursive functions
(d) the set of recursively enumerable languages
(e) the set of C++ programs
Q5 The set of recognising Turing machines does not coincide with proper subsets of which of the following sets?
(a) the set of partial functions
(b) the set of recursive functions
(c) the set of partial recursive functions
(d) the set of recursively enumerable languages
(e) none of the above
Q6 The computational complexity class of languages PTIME, often referred to as P, ...
(a) denotes the set of languages decided by a Turing machine in polynomial time
(b) defines the set of tractably computable algorithms
(c) defines a lower bound on the complexity of Turing machines accepting these languages
(d) all of the above
(e) none of the above
Q7 Does the class LOGTIME exist?
(a) yes
(b) no
(c) yes, but only if Church's thesis holds
(d) no, but only if we assume a TM reads its input
(e) yes, but only if LOGSPACE exists
Q8 Given the diagram below, depicting sets XÍYÍZ and elements aÎX, bÎY, cÎZ, which of the following statements is false?
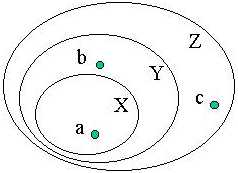
(a) b is X-hard
(b) b is Y-complete
(c) c is Z-hard
(d) b is Z-hard
(e) none of the above


