T Naughton, NUIM
Back to CS370 home

Lab 4 - Decidable languages

In this lab sheet you will prove that particular languages are decidable. We will use Sipser's pseudocode for Turing machines (TMs) from now on. If you have not completed the TM programming problems from the previous lab sheets you should do it in this lab; this will be your last lab to ask for demonstrator help on TM programming.

Example 4.A Consider the language SORT = {(A, B) : A and B are lists of integers, A contains the exact same elements as B, and the elements of B are in ascending order}.

The language SORT is Turing-recognisable. We prove this by showing the existence of the following TM M that recognises SORT.

M = "On input (S₁, S₂) where S₁, S₂ are lists of integers:
      1. Sort B in ascending order.
      2. Compare lists A and sorted B.
      3. If they are the same, accept."

The language SORT is also decidable. We prove this by showing the existence of the following TM M' that decides SORT.

M' = "On input (S₁, S₂) where S₁, S₂ are lists of integers:
      1. Sort B in ascending order.
      2. Compare lists A and sorted B.
      3. If they are the same, accept, if not, reject."

Problem 4.1 Let the language LISTQ = {(A, a, b) : A is a list of integers, a is an integer not in A, b is an integer in A}. (i) Give examples of five words in LISTQ. (ii) Give examples of five words not in LISTQ. (iii) There are an infinite number of words in LISTQ, but is LISTQ countable or uncountable?

Problem 4.2 Prove that LISTQ is Turing-recognisable.

Problem 4.3 Prove that LISTQ is decidable.

Some information about Graphs

A graph is a collection of vertices (nodes) and edges. Consider the following graph G₀.

Each edge joins two vertices together. Some pairs of vertices might not have an edge joining them. For G₀, we could say that the graph contains the set V of vertices where V = {0, 1, 2, 3}. We could also describe the collection of edges as a set. This set E is the set of all pairs (x, y) where both x and y are elements of V, where x y (there is no edge from a vertex to itself), and where x and y are joined by an edge. So for G₀, E would be E = {(0,1), (1,2), (0,2), (0,3)}. Because E is a set, it doesn't matter in what order we write the elements of E. It also doesn't matter what order x and y are in each edge (x, y); the edge (0, 1) is the same as the edge (1, 0). To completely describe G₀ we need to specify both its vertices and edges. So we would say that the graph G₀ is defined as G₀ = (V, E) where V and E are defined above.

A directed graph has arrows on its edges. Here the order of x and y in each edge (x, y) is important. The edge (x, y) means there is an edge from x to y but says nothing about whether there is an edge from y to x. The directed graph G₁ is given below.

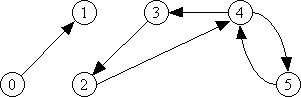
In G = (V, E) notation, G₁ is defined as G₁ = ({0, 1, 2, 3, 4, 5}, {(0,1), (3,2), (2,4), (4,3), (4,5), (5,4)}). Make sure you understand the need for each of these parentheses and braces!

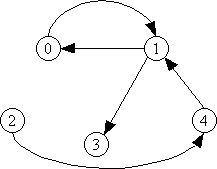
Problem 4.4 Express the following directed graph in G₂ = (V, E) notation.

Problem 4.5 Illustrate what the directed graph G₃ = ({0, 1, 2}, {(0,2), (1,2), (2,1)}) would look like in diagram form.

A path in a graph is a sequence of vertices connected by edges. In G₁ above, we can see that there is a path from 0 to 1, and from 2 to 5, but there is no path from 0 to 3 or from 1 to 0. The path from 5 to 2 would be specified by the sequence of vertices (5, 4, 3, 2) that show you the route you could take from 5 to 2. Without looking at the diagram form of G₁, we can tell there is a path from 5 to 2 because the edges (5,4), (4,3), and (3,2) are present in the set E of G₁.

The path language is defined as PATH = {(G, s, t) : G is a directed graph that has a path from s to t}. So, (G₁, 5, 2) would be in PATH and (G₁, 0, 1) would be in PATH but (G₁, 1, 0) would not be in PATH. (G₁ is defined above.)

Problem 4.6 (i) Is (G₂, 2, 3) in PATH? If so, specify the path as a sequence of vertices.
(ii) Is (G₂, 0, 2) in PATH? If so, specify the path as a sequence of vertices.

Problem 4.7 Let the language NOEDGE = {(G, a, b) : G is a graph, a and b are vertices in G, and there is no edge between a and b}. Prove that NOEGDE is decidable. (Note, a graph is an undirected graph by default. You can assume that any directed graphs will be specifically stated as being directed.)

Problem 4.8 Let the language ISLAND = {(G, a) : G is a graph, a is a vertex in G, and a does not share an edge with any other vertices in G}. Prove that ISLAND is decidable.

Problem 4.9 Let the language ISLANDS = {(G) : G is a graph, and G contains at least one vertex that does not share an edge with any other vertex}. Prove that ISLANDS is decidable.

Problem 4.10 Let the language ONEWAY = {(G) : G is a directed graph, and there is at most one edge between each pair of vertices. I.e., for each arrow in G from vertex a to vertex b there must not be another arrow from b to a}. Prove that ONEWAY is decidable.

Problem 4.11 Let the language NOISLANDS = {(G) : G is a graph, and every vertex has at least one edge connected to it}. Prove that NOISLANDS is decidable.

The following two problems are set as homework for you to figure out.

Homework 4.1 (i) What is the maximum number of edges in a directed graph with 2 vertices?
(ii) With 3 vertices?
(iii) With 4 vertices?
(iv) With 5 vertices? (At this point, you might be quicker working out the equation that describes the relationship between number of vertices in a directed graph and maximum number of edges.)
(v) With 6 vertices?
(vi) With 7 vertices?

Homework 4.2 (i) For this question, consider only directed graphs with a full complement of edges (i.e. an edge between every two vertices, in both directions). We call these fully-connected graphs. A path that goes through every vertex exactly once in a graph with m vertices is a path of length m; it has (m1) edges). What is the maximum number of different paths that go though every vertex exactly once in a fully-connected directed graph with 2 vertices?
(ii) With 3 vertices?
(iii) With 4 vertices?
(iv) With 5 vertices? (At this point, you might be quicker working out the equation that describes the relationship between number of vertices in a directed graph and number of different paths that go through every vertex exactly once.)
(v) With 6 vertices?
(vi) With 7 vertices?