
SE307 - Computation and Complexity Theory
Lab Test 1
Thursday 24 October 2002, 13:00, Lab 4

SE307 - Computation and Complexity Theory
Lab Test 1
Thursday 24 October 2002, 13:00, Lab 4
T Naughton, CS NUIM,
Back to SE307 home
Remove everything from your desk except pens/pencils. Paper will be provided. Turn off all computer monitors. Answer all questions. Remember to be mathematically precise in all of your answers. You have until 14:50. You can leave whenever you are finished.
Note: Finite automata are deterministic by default.
Q1 Construct the state diagram for a finite automaton that accepts the language L = {w : wÎ{a,b}*, w is empty or contains an odd number of as}. [2 marks]
Q2(a) Construct the state diagram for the finite automaton M written formally as M = (Q, S, d, q0, F) = ({0, 1, 2, 3}, {a, b}, d, 0, {1}) where d is
Q\S| a b
---------
0 | 0 0
1 | 2 1
2 | 1 1
3 | 0 1
[2 marks]
Q2(b) What language does the machine in Q2(a) accept? [1 mark]
Q2(c) If we change F to be F={0,1} in the machine in Q2(a), what language does it accept now? [1 mark]
Q3 Describe the language accepted by the finite automaton M = (Q, S, d, q0, F) = ({00, 01, 99}, {0, 1}, d, 00, {99}) where d is
Q\S | 0 1
-----------
00 | 01 00
01 | 99 01
99 | 99 99
[2 marks]
Q4 The state diagram of finite automaton M is given below. Write out the first six words in the lexicographical ordering of the language accepted by M.
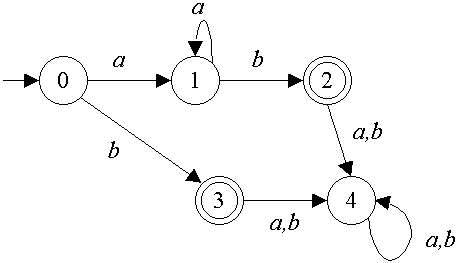 [2 marks]
[2 marks]
Q5 Let finite automaton M be written formally as M = (Q, S, d, q0, F) = ({00, 01, 99}, {a, b}, {((00, a), 00), ((00, b), 99), ((01, a), 00), ((01, b), 01), ((99, a), 00), ((99, b), 99)}, 00, {99}). Construct a table of behaviour of a Turing machine within which the transition function d of M is embedded. State clearly the starting state and accepting states of the resulting Turing machine. [2 marks]