T Naughton, CS NUIM, Back to CS403 home

Q1 One such pushdown automaton is

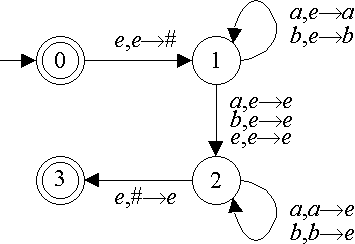
Q2 One possible solution is S->aSa|bSb|a|b|e .

Q3 One possible solution is S->aSa|bSb|#a#|#b#|## . Note, S->aSa|bSb|# would not be an acceptable answer because it fundamentally changes the language (it cuts out palindromes with an odd number of a/b symbols).

Q4 One possible solution proves the existence of a CFL that is also r.e. The proof would go as follows.

Let L={aⁿbⁿ : n>=0}. L is a CFL because it can be generated by the following CFG: S->aSb|e . L is also r.e. because the following (nondeterministic) TM T accepts it. Therefore, there is at least one language in the intersection of the set of CFLs and the set of r.e. languages. The definition of T is T={{00,01,02,03,99},{a,b,_},d,0,{99}} where transition function d is defined as

#Si,R, Sf, W, M
#--------------
00, a, 01, _, R # delete a symbol from the left
00, _, 99, _, R # accept
01, a, 01, a, R # move to the right
01, b, 01, b, R # move to the right
01, _, 02, _, L # position tape head at rightmost symbol
02, b, 03, _, L # delete a symbol from the right
03, a, 03, a, L # move to the left
03, b, 03, b, L # move to the left
03, _, 00, _, R # position tape head at rightmost symbol