T Naughton, CS NUIM

Remove everything from your desk except pens/pencils. Paper will be provided. Turn off all computer monitors. Answer all questions. Remember to be mathematically precise in all of your answers. You have until 11:50. You can leave whenever you are finished.

Name......................................... Student number.........................

Course/year...................................

Q1 What is the tenth word in the lexicographical ordering of the language accepted by FA M given by the following state diagram?

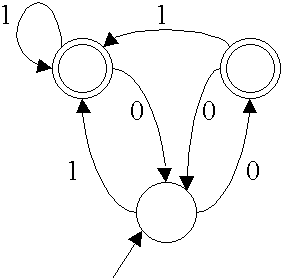
Answer:                                 [1 mark]

Q2 The finite automaton M_a is written formally as M_a = {Q, , , q₀, F} = {{00, 01, 99}, {0, 1}, {((00, 0), 01), ((00, 1), 99), ((01, 0), 01), ((01, 1), 01), ((99, 0), 99), ((99, 1), 99)}, 00, {99}}. Write this finite automaton as a state diagram. [1 mark]

Q3 Fill in the blank (but don't use a regular expression): the language that M_a accepts is L(M_a) = { w :

}. [1 mark]

Q4 Fill in the blank: a regular expression that describes the language L(M_a) is

. [1 mark]

Q5 Construct a FA that accepts the language L = {w : w {0,1}*, w contains an even number of 0s and w ends with 11}. You can either give a formal definition or give a state diagram. [3 marks]

Q6 Give a regular expression that describes L:

[3 marks]

Q7 Construct a FA that accepts the language L' = {w : w {0,1}*, w does not begin with 11 or 00}. You can either give a formal definition or give a state diagram. [3 marks]

Q8 Give a regular expression that describes L':

[3 marks]

Q9 Construct a regular expression that describes the language accepted by the following FA.

Answer:                                 [2 marks]

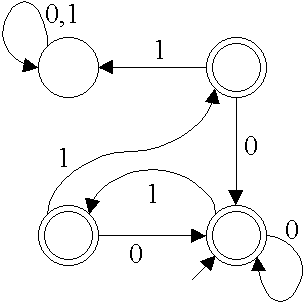
Q10 Use this sequence of steps (given in lectures) to construct an equivalent FA for the following NFA. (Do not remove unused/useless states. Do not simply figure out the language and write the FA from scratch.) [3 marks]

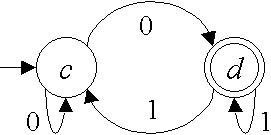
Q11 Let L₁ = {b, aa} and let L₂ = {e, 0, 10}. Assume that in lexicographical order the union of the two underlying alphabets is {0, 1, a, b} (i.e. word a1 comes before word aa in lexicographical order). Write out the first ten words in the lexicographical ordering of (L₁*) L₂. [3 marks]