Abstract
We compress phase-shift digital holograms (whole Fresnel fields) for the transmission of three-dimensional images. For real-time networking applications, the time required to compress can be as critical as compression rate. We achieve lossy compression through quantization of both the real and imaginary streams, followed by a bit packing operation. We define a speedup metric that combines space gains due to compression with temporal overheads due to the compression routine and transmission serialization. We empirically verify transmission speedup due to compression, using a special-purpose Internet-based networking application.

Introduction
Digital holography [1-3] is one of several possible techniques for three-dimensional (3D) imaging. Many existing 3D imaging and processing techniques are based on the explicit combination of several 2D perspectives (or light stripes, etc.) through digital image processing. Multiple perspectives of a 3D object can be combined optically, in parallel, and stored together as a single complex-valued digital hologram. Digital holography has seen renewed interest with the recent development of megapixel digital sensors with high spatial resolution and dynamic range. Their digital nature means that these holograms are in a suitable form for processing or transmission. We record in-line digital holograms using a technique called phase-shift interferometry [3] (PSI), and introduce a third step, that of digital compression and decompression. Each digital hologram encodes multiple views of the object from a small range of angles. Different perspectives of the object can be reconstructed by extracting appropriate regions from the field and applying a numerical propagation technique [3,4].

Our digital holograms have dimensions 2028 X 2044 pixels and in their native format store 8 bytes of amplitude information and 8 bytes of phase information for each pixel. We would like to compress these fields for more efficient storage and transmission. Compression of digital holograms differs to image compression principally because our fields store 3D information in complex-valued pixels, and secondly because of the inherent speckle content which gives them a white-noise appearance. It is not a straightforward procedure to remove the holographic speckle because it actually carries 3D information. The noisy appearance of digital holograms causes lossless data compression techniques (such as Lempel-Ziv-Welch, Huffman, and Burrows-Wheeler) to perform poorly. The use of lossy compression techniques seems essential.

In this article, we apply quantization directly to the complex-valued pixels. We apply a two-stage compression technique based on complex-domain quantization and bit packing. This introduces a third reason why compression of digital holograms differs to compression of digital images; a change locally in a digital hologram will, in theory, affect the whole reconstructed object. We are not interested in how compression noise affects the decompressed digital hologram itself, only how compression noise affects subsequent object reconstruction. In this paper, we use a reconstructed-object-plane RMS metric to quantify the quality of our decompressed digital holograms.

Phase-Shift Digital Holography
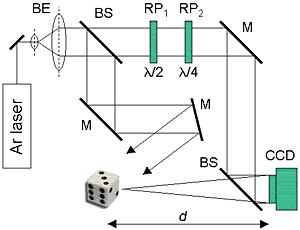
We record digital holograms with an optical system [4,5] based on a Mach-Zehnder interferometer (see Fig. 1). The object beam illuminates a reference object placed at a distance of approximately d =350 mm from a 10-bit 2028 X 2044 pixel Kodak Megaplus CCD camera. Through permutation of the fast and slow axes of the phase retardation plates, RP₁ and RP₂, we can achieve phase shifts of 0, -p/2, -p, and -3p/2. The reference beam combines with the light diffracted from the object and forms an interference pattern in the plane of the camera. At each of the four phase shifts we record an interferogram. We use these four real-valued images to compute the camera-plane complex field by PSI [3]. We call the complex Fresnel field in the camera plane a digital hologram, given a generalized definition of the term hologram.

Fig. 1. Experimental setup for PSI: BE, beam expander; BS, beam splitter; RP, retardation plate; M, mirror.

Compression and Network Transmission
Compression will permit digital holograms to be stored more efficiently. In terms of their transmission, however, there is at least one other property that should be evaluated when comparing compression strategies. We need to know the time it takes, relative to the transmission time, to compress and uncompress the field in order to decide on a compression mechanism for transmission. In particular, it might not even be advantageous to compress the data prior to transmission if the latency caused by the compression routine is significant relative to the average uncompressed transmission time. We consider the case where it is not possible to compress the data in advance, for example in a real-time imaging and transmission application.

In our experiments, the digital hologram window was compressed by the server using a two-step process. The field data was first quantized at a particular resolution. Each pixel of the field data required two data values (real, imaginary). Quantization levels were chosen to be symmetrical about zero; as a result b bits encode (2b-1) levels. For example, two bits encode levels {-1,0,1}, three bits encode levels {-1,-2/3,-1/3,0,1/3,2/3,1}, and so on. The actual data reduction was performed in the second step, where the appropriate b bits were extracted from each quantized real and imaginary value, accumulated in a bit buffer, and packed into bytes.

We quantify the effectiveness of our compression technique in terms of both space and time resource usage by using a measure called speedup. Speedup s is defined as s = P_u / P_c where P_u is the time required to process and transmit the uncompressed digital hologram and P_c is the time required to process, compress, transmit, and decompress the digital hologram. Our timing data is obtained using a special-purpose freely-accessible Internet application that, through the integration of compression and transmission routines into a single application, was able to measure reliably and accurately the interaction between compression times and transmission times.

Fig. 2. Illustration of the network-independent multiple-client system.

Experiments
To determine the quality of the compressed reconstruction we compare it with a reconstruction from an uncompressed digital hologram using a normalized rms (NRMS) difference criterion. A plot of NRMS error against lossy compression through quantization of complex-valued digital hologram data is shown in Fig. 3(a). Quantization at 4 bits results in a compression rate of 16, for low NRMS errors of less than 0.06 in the reconstructed object intensity (with 4 X 4 pixel subsampling). Next we performed the speedup experiments. For several degrees of quantization, and several digital hologram window sizes, a client made requests to the Internet application’s server. Forty trials were recorded for each quantization and each window size. A plot of speedup against compression, for several window sizes, is shown in Fig. 3(b). Incorporating the compression/decompression delays into the transmission timings we observed a speedup of over 9 for window sizes of 512 X 512 pixels and greater. For windows of size 64 X 64 pixels, or greater, there is still significant speedup (over 2.5) for quantizations of 8 bits or lower. Our Internet-based compression application and full timing results are accessible online at http://hologram.cs.may.ie/online/jao2003/hologram.html.

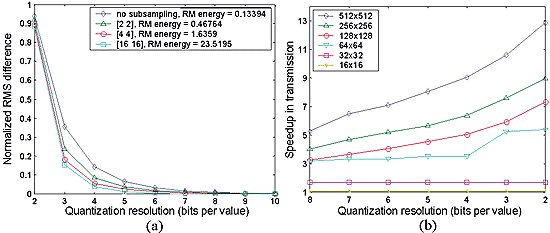Fig. 3(a) NRMS difference in the reconstructed intensity plotted against number of bits in each of the digital hologram's real and imaginary values, for various degrees of subsampling. (b) Speedup as a function of increasing compression, for various digital hologram window sizes.

Conclusion
Digital hologram compression results undeniably make a case for applying compression strategies to the storage of digital holograms. However, in order to be useful for a real-time 3D object capture, transmission, and reconstruction system, the compression strategies must be shown to admit efficient algorithms that make it advantageous to spend time compressing and decompressing rather than simply transmitting the original data. We have defined a speedup metric that combines gains and losses, in both space and time, due to compression and believe that all compression algorithms for real-time or time-critical applications could be evaluated in this way. Our compression technique is based on quantization of real and imaginary components followed by a bit packing operation. The algorithm is efficient (linear in both space and time with respect to the number of holographic pixels) and has been ported for experimentation to a special-purpose Internet-based digital hologram compression application.

Acknowledgement
The authors wish to thank Yann Frauel and Enrique Tajahuerce for the use of their digital hologram data.

References

[1] J.W. Goodman and R.W. Lawrence, Appl. Phys. Lett. 11, pp. 77-79 (1967)

[2] M.A. Kronrod, et al., Sov. Phys. Tech. Phys. 17, pp. 414-418 (1972)

[3] I. Yamaguchi and T. Zhang, Opt. Lett. 22, pp. 1268-1270 (1997)

[4] B. Javidi and E. Tajahuerce, Opt. Lett. 25, pp. 610-612 (2000)

[5] Y. Frauel, et al., Appl. Opt. 40, pp. 3887-3893 (2001)

[6] T.J. Naughton, et al., Appl. Opt. 42, pp. 4758-4764 (2003)

(1) Department of Computer Science, National University of Ireland, Maynooth, County Kildare, Ireland. Email: tom.naughton@may.ie; johnmcd@cs.may.ie

(2) Department of Electrical and Computer Engineering, University of Connecticut, U-157, Storrs, CT 06269, USA. Email: bahram@engr.uconn.edu