The hierarchy of machines and languages that we'll study in the first part of this course began with the work of Gödel, Church, and Turing in the 1930s, and was completed by Kleene, Chomsky, and others in the 1950s.

Section 0: Mathematical preliminaries

Definition 0.0 - A set is a collection of objects. Objects in a set are referred to as its elements. The order of the elements in a set is not important. Elements in a set are not repeated. Elements of a set can be mathematical entities such as numbers and equations, or other things such as animals or songs, or other sets. Therefore {1, a, {1}} and {a, {1}, 1, a} both describe the same set. Sets can be finite or infinitely large. The "size" of a set A is referred to as its cardinality, and is denoted |A|. The cardinality of a set is a natural number (when the set is finite) or (when the set is infinite). We use curly braces {...} to denote a set.

Definition 0.1 - One particular set has a cardinality of zero. This is the empty set or null set. The empty set is denoted or {}.

Definition 0.2 - Set membership and nonmembership are denoted using and 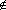, respectively. The statements a {a,b} and c 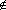{a,b} are true.

Definition 0.3 - A set A whose elements are also elements of a set B is be called a subset of B, denoted by A B symbol. If |B| > |A| then A is called a proper subset of B, denoted by A B. It is true that A A and A for all sets A.

Definition 0.4 - The power set 2^A of a set A is the set of all subsets of A. Let A = {0, 1, 2}, then 2^A = {, {0}, {1}, {2}, {0, 1}, {0, 2}, {1, 2}, {0, 1, 2}}. The notation 2^A for power sets was chosen to remind one of how many elements should be in a power set. For finite sets A, |2^A| = 2^|A|, where 2^x means "raise two to the power of x" when x is a natural number.

Definition 0.5 - The union of two sets A and B, denoted AB is a set that contains each element of A and also contains each element of B.

Definition 1.0 - A sequence or tuple is a collection of elements for which order is important. Elements may be repeated in a tuple. Therefore (1, {2}, 2), ({2}, 1, 2) and (1, {2}, 2, 2) are distinct tuples. We use parentheses (...) to denote a tuple. A tuple of length two is called a pair, a tuple of length three is called a triple, a tuple of length four is called a quadruple, and so on. In general, a tuple of length k is called a k-tuple.

Definition 1.1 - The Cartesian product or cross product of two sets A and B, denoted A 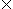B, is the set containing all pairs (p, q) where p A and q B. Let A = {a, b} and let B = {0, 1}. Then A 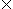B = {(a, 0), (a, 1), (b, 0), (b, 1)}. Similarly, if C = {x, y}, then A 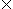B 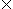C = {(a, 0, x), (a, 0, y), (a, 1, x), (a, 1, y), (b, 0, x), (b, 0, y), (b, 1, x), (b, 1, y)}. The notation A 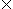B for cross products was chosen to remind one of how many elements should be in a cross product. For a finite number of finite sets A₀, A₁, ..., A_n, the cardinality of their cross product |A₀ 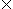A₁ 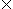... 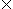A_n| = |A₀| . |A₁| . ... . |A_n| where "." means multiplication.

Definition 1.2 - Where the elements of a set are sequences, an operator similar to Cartesian product exists that is called concatenation. The concatenation of two sets A and B, where those sets contain sequences, and denoted A o B, is the set of all sequences that can be formed by concatenating one element from A with one element from B. For example, {(a, b), (b)} o {(x, y), (y)} = {(a, b, x, y), (a, b, y), (b, x, y), (b, y)}. The concatenation of three sets A o B o C is a set that contains sequences that are the concatenation of three sequences each. One way that concatenation is distinct from Cartesian product is that sometimes the cardinality of the concatenation of sets is not the same as the cardinality of the Cartesian product of those sets, for example {(a), (a, a)} o {(a), (a, a)} only contains three elements, whereas the Cartesian product of two sets of two elements each always contains four elements.

Definition 1.3 - A relation on sets A and B is a subset of A 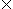B. Let A = {a, b}, B = {0, 1}, then {(a, 0)}, , and {(b, 0), (b, 1)} are all relations on A and B. A relation on two sets (as in this case) is called a binary relation.

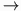Definition 1.4 - A function from A to B is a binary relation between A and B where only one tuple (a, b) exists for each a A. A function f : A B can be regarded as mapping elements in A to elements of B. A is referred to as the domain and B is referred to as the range. Each element in A maps to exactly one element in B. Multiple elements of A may map to the same element in B, and not every element of B needs to be mapped by an element of A. 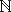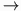The function square : 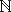maps natural numbers to their squared value. This function could be defined by a procedure such as square(a) = a.a, or by listing all possible tuples of inputs and outputs. For example, the function sum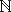4 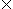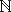: _{4 4 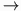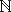4} maps pairs of naturals from 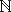₄ = {0, 1, 2, 3} to their sum modulo 4. The function could be defined by sum(i, j) = (i + j) mod 4, or equivalently by the following table.
sum(i,j)=
i\j | 0 1 2 3
----|--------
  0 | 0 1 2 3
  1 | 1 2 3 0
  2 | 2 3 0 1
  3 | 3 0 1 2
A relation on A and B could also be specified as a function f : A 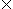B 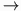{TRUE, FALSE} where the inclusion of a tuple in the relation is signified by that tuple mapping to TRUE.

Definition 2.0 - A symbol is a single character such as a letter or digit.

Definition 2.1 - An alphabet (usually denoted with ) is a nonempty finite set of symbols. (A nonempty finite set is a set that has a finite number of elements and has more than zero elements.)

Definition 2.2 - A string or word is a tuple of symbols. For this module, all words have finite length. The length of a word w is denoted |w|. A word over an alphabet is a word made up of symbols from . For example, let = {a, b}, then (a, b, a) is a word over . The zero-length word (empty word) is a word over any alphabet. The empty word is usually denoted e. To avoid confusion, you should take care not to define any alphabets that contain "e" as a symbol. Because each symbol in a word is one character long, we can usually omit the parentheses and commas when specifying a word. So, in the above example, we could simply say that aba is a word over .

Definition 2.3 - The set of all words over an alphabet is denoted *. For example, let = {a, b}, then a *, bb *, aaabab *, and so on. We adopt a convention when listing the words in a set. It is called lexicographical order. This means listing shorter words first, and if several words have the same length, then list them in alphabetical order (usually the symbols in an alphabet will have an implicit alphabetical ordering, for example the order in which they are written down when you first encounter them). Writing * in lexicographical order gives * = {e, a, b, aa, ab, ba, bb, aaa, aab, aba, abb, baa, bab, bba, ...}. For all nonempty , * is infinite. Note that this implies that * always contains e, regardless of what the set contains, and in particular even if is empty.

Definition 2.4 - A language is a set of words. A language may be infinite. A language may be empty. A language over an alphabet is a subset of *.

Definition 2.5 - A machine accepts or recognises a language L if it outputs TRUE (or goes into an appropriate state) if and only if (iff) it is presented with a word w L. It does not matter what the machine does if it is presented with a w 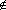L (as long as it doesn't also accept it).

Section 1: Language theory

Why do we use languages to study the power of computing devices? Well, think of all the varied computations that can be performed with a computer... think of all the different inputs and outputs. How could we represent all possible computations within a single framework such that we could make some meaningful comparisons between diverse computations? Such as, is the problem of formatting a page of text more complicated than a building a spreadsheet program? Or, is calculating the compound interest on a loan more complicated than the actions of a webserver? Or is solving Minesweeper(TM) as complicated as air traffic control?

Language theory gives us such a framework. Every single computational problem can be expressed as a language acceptance problem. Quite often the words of the language are formed from input-output pairs of the computation in question. By being able to tell if it has been given a valid input-output pair, a machine has demonstrated that it has the capability to compute the function that generated the input-output pairs in the first place. Although it would undoubtedly take longer to compute the pairs than validate them, this is not relevant to the issue of sufficient computational power.

Example. Addition. Your machine can perform addition over 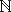iff it can accept the language L of the words that have the form of a 3-tuple of natural numbers where the third number is the sum of the first two. This language could be described more formally as L = {w : w = (a, b, c), a, b, c 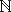, (a + b) = c} = {(0, 0, 0), (0, 1, 1), (1, 0, 1), (1, 1, 2), (1, 2, 3), ...}

Example. Translation. Your machine can translate between English and Finnish iff it can accept the language of words that have the form of a pair of sentences (one from English, one from Finnish) where both sentences have the same meaning. L = {("Hello", "Hei"), ("I'm hungry", "Minula on nälkä"), ...}

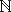
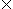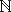
Example. PI. Your machine can calculate iff it can accept the language L of words of the form ( {.}), where the first number in the pair is an index and the second is the symbol at that index in the infinite decimal representation of . So, L = {(0, 3), (1, .), (2, 1), (3, 4), (4, 1), (5, 5), (6, 9), ...}.

Therefore, one of the central issues in the theory of computation is the representation of languages by finite descriptions. It is interesting to note that each description itself will be a sequence of symbols. If we treat each description (sequence of symbols) as a word itself, what language does it form?

Those languages that have a finite representation could be regarded as corresponding to problems that have finite set of unambiguous and non-contradictory formal requirements. These are exactly the types of problems that we would expect a computer could be programmed to solve. By investigating what are the most complicated languages a computer can accept, we can begin to understand the limits of computers. Unfortunately, but importantly, we'll see that we can prove quite easily that some very simple problems with unambiguous and non-contradictory formal requirements defy any computer program solution. We'll first look at very simple computers, progressively making them more sophisticated, until we have a definition for the simplest computer that can do anything that the world's most sophisticated computer can do. To begin our study, we'll consider the simplest class of machines. These are the deterministic finite automata, and they specify the regular languages.