T Naughton, MU
Back to CS605 home

Laboratory sheet - Turing machine programming

With this lab sheet you will develop some basic Turing machine (TM) programming skills. The lab sheet consists of solved example TM problems that you should try to fully understand, and unsolved problems that you should use to test your knowledge.

You can use Paul Ming's Virtual Turing Machine (VTM) to test your machines; it gives a trace of every step in the computation. Open it up in a separate browser to give yourself some comfort. I have written the following TMs to conform to the VTM's convention. If you require a definition of any symbols (for example, '#' means the beginning of a comment) see the VTM introduction page. Note: the VTM only works with deterministic TMs.

Example Machine 2.A This TM takes a single word on its input tape, and writes a `T' on the tape if the input word is in the language {a,b}. Assume that our tape head is automatically positioned at the beginning of the input initially.

Solution. One valid table of behaviour corresponding to such a machine would be as follows. The start state is 00.

#Si,R, Sf, W, M
#--------------
00, a, 01, a, R # state 01 means we have found at least one `a'
00, b, 01, b, R # state 01 also means we have found at least one `b'
01, _, 99, T, R # there was only one `a' or `b', so accept

Copy and paste this machine into the VTM with the following sample inputs (without quotes):
Tape: "___a___"
Blank: "_"
Initial: "00"
Run it with the following options "one line per step", "show state before tape", and "show form after results".

Use the trace to follow the evolution of the computation (the angled brackets indicate the position of the tape head at each step). Try a few inputs of your own, including "___aa___", "___b___", "___ab___", "___bab___", and "_____".

NOTE: Make sure to put two or three blank symbols "_" on either side of input to simulate an infinite tape. The VTM automatically positions the TM head at the first non-blank symbol in the input, or at the centre of the input if it contains only blank symbols.

Example Machine 2.B In this example, we'll write a `T' if the single word on our input tape contains one or more copies of the symbol `a' (and no other symbols). That is, we will accept the language given by the regular expression aa*. As always, assume that the tape head is positioned at the beginning of the input initially.

Solution. One valid table of behaviour is (the start state is 00):

#Si,R, Sf, W, M
#--------------
00, a, 01, a, R # we have found our first `a'
01, a, 01, a, R # we have found another `a'
01, _, 99, T, R # there were only copies of `a' so accept

Use the trace to follow the evolution of the computation. Inputs such as "___aaa___" and "___a___" should be successful, and "______" and "___aaaba___" should not.

Example Machine 2.C An even simpler machine is one that checks if the single input word contains zero or more copies of `a' (and no other symbols). That is, a machine that accepts the language given by the regular expression a*.

Solution. One valid table of behaviour is (the start state is 00):

#Si,R, Sf, W, M
#--------------
00, a, 00, a, R # we have found another `a'
00, _, 99, T, R # no non-`a's so accept

Inputs such as "______" and "___aaaa___" should be successful, and "___x___" and "___aaaba___" should not.

Example Machine 2.D Same as Machine 1.B, except we must also ensure that we write an `F' if our input word contains any non-`a' characters or is blank. Here, we are deciding the language rather than accepting/recognising it as before. Assume that the input alphabet is {a,b}. For example, input words "aaa" and "a" should result in a `T'. Input words "aaab" and "abaaaa" should result in an `F'. (Don't forget to remove the quotes and put blanks on either side of these sample inputs.)

Solution. One valid table of behaviour corresponding to such a machine would be as follows. [One hint for building deciding TMs: it is always a good idea to have a row in your table of behaviour for every combination of non-halting state and alphabet symbol (plus the blank symbol). This means (Q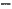F)(+1) rows in most cases. That way you can be sure your TM will never crash outside of a halting state.] The start state here is 00.

#Si,R, Sf, W, M
#--------------
00, _, 99, F, R # if the input is empty then reject
00, a, 01, a, R # state 01 means we found at least one `a'
00, b, 99, F, R # `b' found as the first symbol, so reject
01, a, 01, a, R # found another `a' so stay in this state
01, b, 99, F, R # `b' found somewhere , so reject
01, _, 99, T, R # there were only `a's so accept

Example Machine 2.E Next, we'll construct a TM that doesn't accept any particular language, but performs a transformation from each input word to another word. In this case, the input alphabet is {a,b} and the transform is f:{a,b}*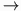e (it simply deletes its input). As always, assume that the tape head is positioned at the beginning of the input.

Solution. One valid table of behaviour is (the start state is 00):

#Si,R, Sf, W, M
#--------------
00, _, 99, _, R # when we reach a blank we halt
00, a, 00, _, R # we have found another `a'
00, b, 00, _, R # we have found another `b'

As always, try a few inputs of your own, such as "___aaa___", "___abb___", and "_____".

Example Machine 2.F Construct a TM that changes all of the symbols in its input word to `a's. Formally, the TM performs the transformation f:{a,b}*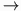{a}* where f is defined as f(x)=a^|x|. For the initial state of the computation, assume that the tape head is positioned at the beginning of the input (for example, "abb", where the underscore represents the position of the TM tape head). When the TM halts, the tape head should be positioned at the beginning of the input word (in this case, "aaa"). One valid table of behaviour corresponding to such a machine would be as follows. (The start state is 00.)

Note: if the comments in the TM below do not fit on a single line when you paste them into the VTM, then you should shorten or delete them.

#Si,R, Sf, W, M
#--------------
00, _, 01, _, L # when we reach a blank, we're at the end of the word so step left
00, a, 00, a, R # if we encounter an `a', just step right
00, b, 00, a, R # if we encounter a `b', replace it and step right
01, a, 01, a, L # if we're in state 01 we're in the process of returning to the beginning of the word
01, _, 99, _, R # when we reach the blank to the left of the word, just step right

Try a few inputs of your own, including "____abab____", "____b____", and "______".

Example Machine 2.G Construct a TM to increment a unary number. (Here, unary numbers are represented by words that contain zero or more `1' symbols.) It therefore performs the transformation f:{1}*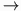{1}* where f(x)=x1. Assume the tape head is positioned at the beginning of the input initially (for example, "111", where the underscore represents the position of the TM tape head). At the end of the computation, the tape head should have positioned itself at the beginning of the output (in this case, "1111"). One valid table of behaviour corresponding to such a machine would be as follows. (The start state is 00.)

#Si,R, Sf, W, M
#--------------
00, 1, 00, 1, R # while looking for the end of the word, keep stepping right
00, _, 01, 1, L # when we reach the end of the word, write a `1' and step left
01, 1, 01, 1, L # while looking for the beginning of the word, keep stepping left
01, _, 99, _, R # when we reach the beginning of the word, step right and halt

Try a few inputs of your own, including "____1111____", "____1____", and "______".

Machine 2.1 Construct a TM that changes all of the `a' symbols in its input word to `b', and all of its 'b' symbols to `a'. Assume that the input word is an element of {a,b}*. For example, an input "abaab" should be transformed into "babba".

Machine 2.2 Construct a TM that writes a `T' if the input word contains the substring "aa". Assume that the input word is an element of {a,b}*. For example, inputs "abaaba" and "aa" should cause the TM to write a `T', and input "ababa" should not cause it to write a `T'.

Machine 2.3 Construct a TM to add 3 to a unary number. Assume the tape head is positioned at the beginning of the input initially (for example, "11"). At the end of the computation, the tape head should have positioned itself at the beginning of the output (in this case, "11111").

Machine 2.4 Construct a TM that accepts the language L = {w : w{a,b}*, w ends with the substring aab}. Your TM should halt in state 99 iff the input word is in L. If the input word is not in L, it does not matter what your TM does, as long as it does not halt in state 99.

Machine 2.5 Modify the previous machine so that it decides the language. Your TM must accept words in L and reject words not in L. Let 99 be your accepting state and let 50 be your rejecting state. Your Turing machine should always halt in one of these states if it is given a word in {a,b}*. Furthermore, the tape head must be back at the start of the word when your TM halts.

Machine 2.6 Construct a TM to increment a binary number. Assume each input word is an element of (0 1)(0 1)*. For example, input "1000" should be transformed into "1001", input "1001" should be transformed into "1010", input "1111" should be transformed into "10000", and so on.

Example Machine 2.H Write a TM that accepts the language L = {w1w : w{0}*}. To accept a word the TM should go into state 99.

So, in lexicographical order, L = {1, 010, 00100, 0001000, 000010000,...}. Also, note that because the question doesn't specifically ask us not to delete the input, it is OK for us to delete it if we want.

Sample solution (in pseudocode).

On input word w:
1) Remove a 0 from the left end of the word and a 0 from the right end of the word
2) Keep repeating this as long as you can, making the word shorter and shorter
3) If you are left with a single 1, then accept

This sample solution again (this time expressed as a TM table of behaviour). The start state is 00.

#Si,R, Sf, W, M
#--------------
00, 0, 01, _, R # remove a 0 from the left end
01, 0, 01, 0, R # move to end of word
01, 1, 01, 1, R # move to end of word
01, _, 02, _, L # at end of word step left
02, 0, 03, _, L # remove a 0 from the right end
03, 0, 03, 0, L # move back to beginning of word
03, 1, 03, 1, L # move back to beginning of word
03, _, 00, _, R # at beginning of word, start all over again
00, 1, 04, _, R # no more zeros on the left, so check on right
04, _, 99, _, R # no more zeros on right either, so accept

Try a few inputs of your own, including "____010____", "____1____", and "___000010000___" (which should all be accepted), and "____00____", "________", "____001000____", and "___000100___" (which should not be accepted -- i.e. should halt in any state except 99).

Example Machine 2.i Write a TM that accepts the language L = {w : w{0,1}*, |w|>=1, w begins and ends with the same symbol}. In lexicographical order, L = {0, 1, 00, 11, 000, 010, 101, 111, 0000, 0010, 0100, 0110,...}. To accept a word the TM should go into state 99.

Sample solution (in pseudocode).

On input word w:
1) Remember if the first symbol is 0 or 1
2) Skip to the end of the word
3) If the same symbol is at the end, then accept

This sample solution again (this time in TM code). The start state is 00.

#Si,R, Sf, W, M
#--------------
00, 0, 01, 0, R # state 01 means we read a 0
00, 1, 02, 1, R # state 02 means we read a 1
01, 0, 01, 0, R # move to end, remembering we read 0
01, 1, 01, 1, R # move to end, remembering we read 0
01, _, 03, _, L # move to final symbol, remembering we read 0
02, 0, 02, 0, R # move to end, remembering we read 1
02, 1, 02, 1, R # move to end, remembering we read 1
02, _, 04, _, L # move to final symbol, remembering we read 1
03, 0, 99, 0, R # it was the appropriate symbol, so accept
04, 1, 99, 1, R # it was the appropriate symbol, so accept

Machine 2.8 Modify the code of Example Machine 2.i so that it decides the language. To reject a word the TM should go into state 50.

Machine 2.9 Construct a TM that decides the language of binary palindromes (words that read the same forwards as in reverse). Formally, this is the language L = {w : w{0,1}*, w=w^R}. In lexicographical order, L = {e, 0, 1, 00, 11, 000, 010, 101, 111, 0000,...}. To decide this language, the TM must halt in state 99 iff the input is in L. Otherwise the TM must halt in state 50.

Machine 2.10 Construct a TM that decides the language L = {w{0,1}* : w has an equal number of 0s and 1s}. Therefore, L = {e, 01, 10, 0011, 0101, 0110, 1010, 1100, 000111, 001011, 001101, 001110, ...}.

Machine 2.11 Modify the code of Example Machine 2.H so that when the TM halts the tape head is at the beginning of the input word. (This means you can't delete the input! Hint: rather than overwriting the 0s with blanks, try overwriting them with an 'x' and then as a final step replace all 'x's with 0s again.)

Machine 2.12 Construct a TM that accepts L={w : w=axbxc, a,b,c{1}*, |a|+|b|=|c|}, which is a language equivalent to the problem of addition over 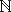. In lexicographical order, L={xx, x1x1, 1xx1, 1x1x11, 1x11x111, 11x1x111, 11x11x1111, 11x111x11111,...}. To accept this language, the TM must halt in state 99 iff the input word is in L.